Blog do Guilherme

Procedimentos e processos - o modelo da substituição

Introdução

Este post surgiu após assistir a aula “Lecture 1B: Procedures and processes; Substitution model” do curso MIT 6.001 Structure and Interpretation, de 1986.

its the poster for “Structure & Interpretation of Computer Programs” by Harold Abelson and Gerald Jay Sussman. It features a wizardly man with a gray, long beard, and a purple robe with stars

Se você não conhece, esse curso é baseado no livro Structure and Interpretation of Computer Programs e foi lecionado pelos próprios autores :).

Na aula, vemos como utilizar o modelo da substituição (substituition model) para entender como um computador avalia uma aplicação, e, em especial, aplicações com implementações recursivas.

Modelo da substituição

Aplicações são algoritmos, ou conjunto de regras utilizadas para realizar cálculos e manipulações numéricas.

Os algoritmos são compostos de diversas expressões:

*: Estes são casos especiais que possuem regras específicas.

Como números são avaliados como eles mesmos (um 7 é interpretado como o valor 7 pelo computador), e, no modelo da substituição, os símbolos são removidos, a compreensão do modelo depende da forma como avaliamos combinações.

Regra da substituição

Para avaliar uma aplicação
- Avalie o operador para conseguir o procedimento
- Avalie os operandos para conseguir os argumentos
- Aplique o procedimento aos argumentos
— Copie o corpo do procedimento, substituindo os argumentos fornecidos pelos parâmetros formais do procedimento.
— Avalie o novo corpo resultante.

A soma de dois quadrados

O exemplo inicial é a soma de dois quadrados: dados dois números, calcule a soma de seus quadrados.

(define (sos x y) (+ (square x) (square y)))

(define (square x) (* x x))

(sos 3 4)
// 25

Aplicando a regra da substituição, começamos avaliando os operandos, ou seja, substitutuindo x por 3, e y por 4.

(sos 3 4)
(+ (square 3) (square 4))
(+ (square 3) (* 4 4))
(+ (square 3) 16)
(+ (* 3 3) 16)
(+ 9 16)
// 25

Condicionais

Existem regras específicas referentes às expressões condicionais.

Para avaliar uma expressão IF
- Avalia a expressão do predicado (predicate)
-- Se ela for VERDADEIRA
--- avalie a expressão consequente (consequent)
-- Se não
--- avalie a expressão alternativa (alternative)

Na sintase do lisp, temos algo no formato:

(if <predicate>
    <consequent>
    <alternative>)

O funcionamento do if pode ser ilustrado através de um programa, a soma de x e y, feito através da aritmética de Peano, limitada a operações de adição e subtração.

(define (sub1 x) (- x 1))

(define (incr1 x) (+ x 1))

(define (add x y)
  (if (= x 0)
    y
    (add (sub1 x) (incr1 y))))

(add 3 4)
// 7

Repare que a função add é recursiva: ela chama a si mesma até atingir uma condição (quando x for 0), momento no qual ela retorna um valor específico (y), quebrando o loop.

Podemos compreender a função add melhor aplicando a subsituição:

(add 3 4)
// x é diferente de zero
(add (sub1 3) (incr1 4))
(add (- 3 1) (+ 4 1))
(add 2 5)
// x ainda é diferente de zero
(add (sub1 2) (incr1 5))
(add (- 2 1) (+ 5 1))
(add 1 6)
// x ainda é diferente de zero
(add (sub1 1) (incr1 6))
(add (- 1 1) (+ 6 1))
(add 0 7)
// x é igual a zero!! retornamos y (7)

Intuição - recursividade e iteração

De acordo com o livro, um procedimento é um padrão para a evolução local de um processo computacional. Esses padrões podem ser descritos em função de como eles consomem recursos computacionais de espaço e tempo.

A procedure is a pattern for the local evolution of a computational process. It specifies how each stage of the process is built upon the previ- ous stage. We would like to be able to make statements about the overall, or global, behavior of a process whose local evolution has been specified by a procedure. This is very difficult to do in general, but we can at least try to describe some typical patterns of process evolution.

O algoritmo add demonstrado anteriormente tem a seguinte evolução:

----------> space

(add 3 4) |
(add 2 5) |
(add 1 6) | time
(add 0 7) |
7         v

Caso aumentarmos o problema somando, por exemplo, 4 e 4, o algoritmo iria precisar de um passo adicional, aumentando, linearmente, o tempo de execução.

O eixo vertical pode ser entendido como o tempo necessário para a execução do algoritmo, enquanto o eixo horizontal pode ser entendido como o quanto o computador precisa lembrar para executar um passo (também chamado de espaço ou memória).

O algoritmo add pode ser descrito como possuindo complexidade linear de tempo, O(x), e complexidade constante de espaço, O(1).

Uma versão alternativa do mesmo algoritmo pode ser implementado da seguinte forma:

(define (sub1 x) (- x 1))

(define (incr1 x) (+ x 1))

(define (add_alt x y)
  (if (= x 0)
    y
    (incr1 (add_alt (sub1 x) y))))

(add_alt 3 4)
// 7

Ele revela o seguinte padrão ao aplicarmos a substituição:

(add_alt 3 4)
// x é diferente de zero
(incr1 (add_alt (sub1 3) 4))
(incr1 (add_alt 2 4))
// x segue diferente de zero
(incr1 (incr1 (add_alt (sub1 2) 4)))
(incr1 (incr1 (add_alt 1 4)))
// x ainda é diferente de zero!
(incr1 (incr1 (incr1 (add_alt (sub1 1) 4))))
(incr1 (incr1 (incr1 (add_alt 0 4))))
// x é zero! podemos retornar o valor de y
(incr1 (incr1 (incr1 4)))
// agora vamos aplicando os incrementos
(incr1 (incr1 5))
(incr1 6)
7

Se focarmos apenas na evolução do algoritmo, temos esse padrão:

(add_alt 3 4)                      \
(incr1 (add_alt 2 4))               \
(incr1 (incr1 (add_alt 1 4)))        \
(incr1 (incr1 (incr1 (add_alt 0 4)))) |
(incr1 (incr1 (incr1 4)))            /
(incr1 (incr1 5))                   /
(incr1 6)                          /
7                                 /

O formato de expansão seguida de contração ocorre quando temos um aumento de operações deferidas (neste caso, as operações de incremento). A contração ocorre conforme as operações são realizadas.

O algoritmo add_alt possui complexidade linear no tempo, O(x).

Devido ao aumento, até certo ponto, do espaço necessário para a execução do programa, a sua complexidade no espaço é linear, O(x). Para cada valor de x vai existir uma operação de incremento deferida, que deve ser salva na memória do computador para execução posterior.

Este tipo de processo é denomeado processo recursivo. Para que seja realizado o interpretador precisa manter um registro das operações que devem ser realizadas no futuro.

No exemplo acima, o número de incrementos cresce linearmente com o valor de x passado na função (é proporcional a x), e, portanto, pode ser chamado de um processo linearmente recursivo.

No primeiro exemplo não existe essa expansão/contração. Em cada passo, toda informação que precisamos está explícita nos argumentos x e y da função.

(add 1 6)

Esse tipo de processo é chamado de processo iterativo. Um processo iterativo é um no qual o seu estado pode ser descrito por um número fixo de variáveis de estado, juntos à uma regra fixa que define como as variáveis de estado devem ser atualizadas conforme o processo evolui de passo a passo.

Na nossa função add, o número de passos cresce linearmente com x (pois é x que define o critério de parada da função, quando x = 0). Pode ser chamado, portanto, de processo linearmente iterativo.

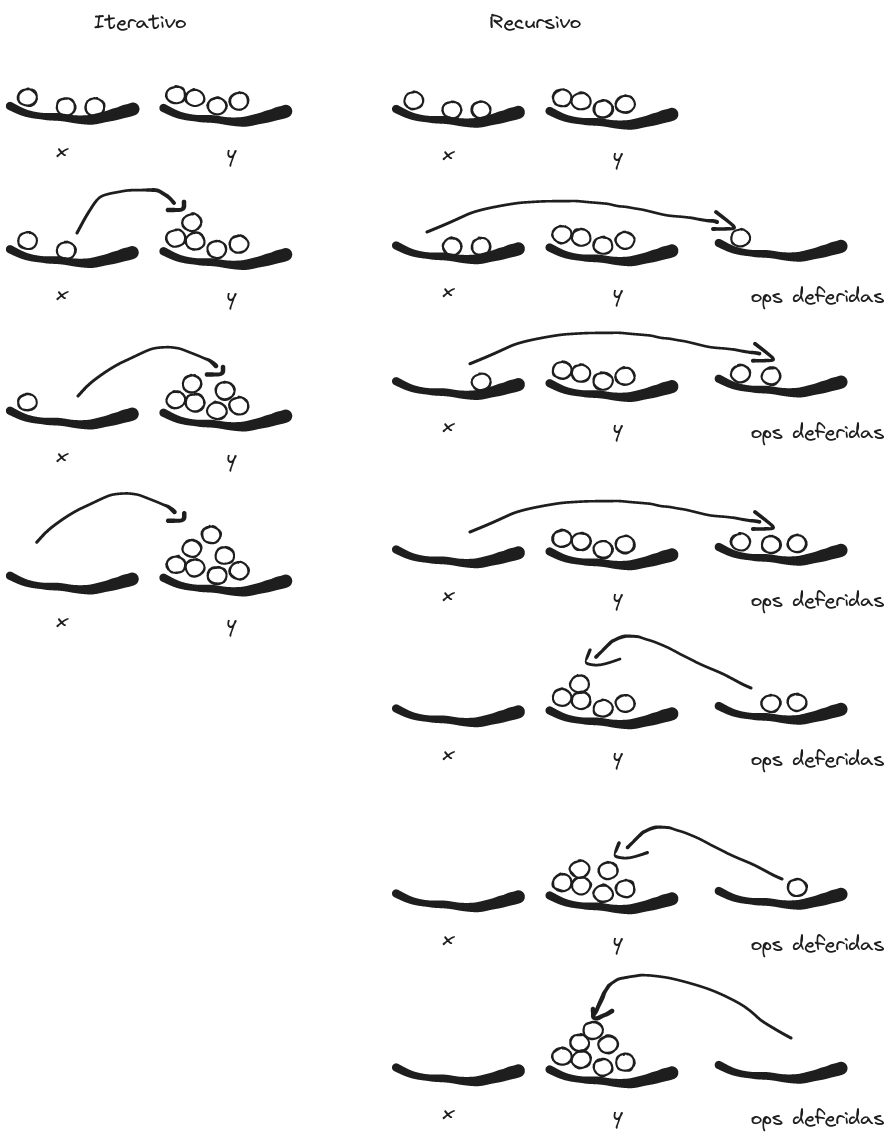
Formas de visualizar operações iterativas vs. recursivas para o algoritmo de adição: na iterativa, as bolas (valores) são passados diretamente de uma pilha (x) para outra (y), enquanto na recursiva elas são primeiro enviadas para uma terceira pilha (operações deferidas), e depois dessa pilha para a pilha y.

Diferentes formas de recursão

Acima vimos duas funções, add e add_alt. As duas chegam no mesmo resultado, agindo de forma recursiva (ambas chamam a si mesmas), mas com formatos de execução diferentes.

É importante ressaltar que o fato de uma função ser definida de forma recursiva não implica que o seu processo ocorra de forma recursiva. A função add, por exemplo, exibe um processo linearmente iterativo.

Pra esclarecer melhor essa diferença, trago um exemplo usando Python: vamos supor uma função sum_up_to(value) que soma todos os valores, de 1 até value, e retorna o resultado.

def sum_up_to(value):
  total = 0
  while (value) > 0:
    total += value
  return total

print(sum_up_to(10))
# 55

Caso queiramos reimplementar essa função de forma recursiva, uma possível implementação é a seguinte:

def sum_up_to(value):
  if value > 0:
    return value + sum_up_to(value - 1)
  return value

Essa implementação tem um processo linearmente recursivo. Usando o método da substituição, podemos ver o padrão da função:

sum_up_to(10)
10 + sum_up_to(9)
10 + 9 + sum_up_to(8)
10 + 9 + 8 + sum_up_to(7)
# ...
10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
# 55

A sua complexidade no tempo é linear com o valor da entrada value, O(x), assim como sua complexidade no espaço, O(x).

Uma implementação alternativa, também usando recursividade, seria utilizando variáveis de estado pra mantermos, a cada passo, todos os valores necessários pra chegar no próximo ponto, sem precisar deixar isso por conta do interpretador:

def sum_up_to(value, total):
  total = total + value
  value -= 1
  if value > 0:
    return sum_up_to_rec(value, total)
  return total

O padrão da função é levemente diferente:

sum_up_to(10, 0)
sum_up_to(9, 10)
sum_up_to(8, 19)
sum_up_to(7, 27)
sum_up_to(6, 34)
# ...
sum_up_to(1, 54)
sum_up_to(0, 55)
# 55

Enquanto a complexidade no tempo segue sendo linear com o valor de entrada value, a sua complexidade no espaço é constante, O(1). O processo resultante dessa segunda implementação é linearmente iterativo.

#português #algoritmos #lisp #python